行测辅导资料
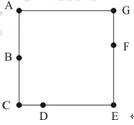
已知在如下图所示的正方形ACEG的边界上有7个点A、B、C、D、E、F、G，其中B、D、F分别在边AC、CE、EG上。如果以这7个点的4个点为顶点组成的不同的四边形共有多少个？
A.23
B.27
C.31
D.35
A.72
B.78
C.82
D.142
小明和小强参加同一次考试，如果小明答对的题目占题目总数的3/4，小强答对了27道题，他们两人都答对的题目占题目总数的2/3，那么两人都没有答对的题目共有（ ）。
A.3道
B.4道
C.5道
D.6道
甲、乙两个科室各有4名职员，且都是男女各半，现从两个科室中选出4人参加培训，要求女职员比重不得低于一半，且每个科室至少选 1人，问有多少种不同的选法？
A.67
B.63
C.53
D.51
有一种数叫做完全数，它恰巧等于除去它本身以外的一切因数的和，如6个因数1+2+3的和。请问在20～30之间，这样的完全数是哪个？（ ）
A.24
B.26
C.27
D.28
1.答案:
解析: 根据题意，从7个点中选出4个点共有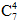
=35种方法，由于当四边形的三个点在一条直线上时，就不能组成四边形，共有3×4=12种情况，即公有35-12=23种方法。
2.答案:
解析:
时钟总共发出的响声次数等于整点时钟发出的响声次数加上每个半点时时钟发出的响声次数，时钟从某一日上午6：45分走到下午17：20，所走过的整点时刻有7、8……12、1、2……5。因此发出的整点响声次数=1+2+3+…﹢12－6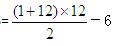
=72(次)。再加上每个半点时发出的响声次数，包括7：30、8：30……16：30，共16－7+1=10(次)。因此时钟总共发出82次响声。
3.答案:
解析:
由“小明答对的题目占题目总数的3/4”，可知题目总数是4的倍数；由“他们两人都答对的题目占题目总数2/3”，可知题目总数是3的倍数。因此，题目总数是12的倍数。小强做对了27题，超过题目总数的2/3，则题目总数是36。根据两集合容斥原理公式得两人都没有答对的题目共有36－（36×3/4＋27－36×2/3）＝6道，故正确答案为D。
4.答案:
解析:
5.答案:
解析:
直接代入验证，只有D符合条件，28的因数为1、2、4、7、14，28＝1＋2＋4＋7＋14，故正确答案为D。
