公务员考试资料 事业单位数量关系的题另大部分同学比较头疼的题目，部分题目在求解过程中比较复杂，导致计算时间较长，单位时间内做出的总体题目数量较少最终导致整体得分不尽如人意，今天介绍一种解题方法：特值法。希望通过学习能给大家带来一些启发，在一定程度上提高做题的效率。
一、特值法的应用条件
特值法一般是在包含乘除法的题目中应用的一种方法，应用条件为：①存在M=A×B关系;②对应量未知。
1、存在M=A×B关系：指的是在数量关系中的一些计算关系，如行程问题中S=V×T、工程问题中W=P×T、总价=单价×数量、长方形的面积=长×宽……
2、对应量位置：举例说明
例：一项工程，甲单独做需要10天完成，乙单独做需要15天完成，问甲乙合作需要几天完成?
解：题目所求为工作时间，根据公式W=P×T，T=W/P其中工作总量，工作效率都未知，可以设其中W=x，根据甲单独完成需要10天，可知甲的效率为x/10;同理可知乙的效率为x/15，则最终所求的合作时间T=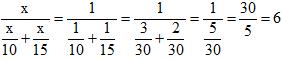
，研究计算过程，我们发现：设的工作总量x，其实在计算过程中没有起实质的作用，在计算过程中约分约掉了，那就可以理解为我们可乙将工作总量设为任意数字，如假设工作总量为30，可以计算出甲的效率为30÷10=3，乙的效率为30÷15=2.最终所求工作时间为30/(3+2)=6。
总结：根据计算公式W=P×T，和题目中给的两个时间，如果设W为一个数，另外一个量工作效率P会通过公式计算得到一个数值，但是计算的结果不发生变化。如果题目中对应有两个量已知，如工作时间10天、工作效率为5，则工作总量必然为50。此时如果再设特值，肯定要出问题了。所以应用条件中对应量未知表示的是M=A×B中，至少有两个量未知时才可设特值进行求解。如果有两个量未知，可设其中一个量为特值，计算出第三个量;如果其中三个量都未知，可设其中两个量为特值进而计算出第三个量。
例：某商店销售某种商品，当销售单价下降20%时，销售量可增加50%，问该商品降价后总销售价格比降价前增加/减少百分之几?
解：根据题意，总售价=单价×销售量，满足第一个条件：存在乘除关系，而题目中单价、销售量和总售价的实际量都是未知的，满足第二个条件：对应量未知，可设特值进行求解。可设降价前单价为10元/件、销售量为10件，根据计算关系可知降价前总售价=10×10=100元，根据条件降价后单价为8元/件、销售量为15件，此时总售价=8×15=120元，所以该商品降价后总销售价格比降价前增加(120-100)/100=20%。
最后，希望大家加强对特值法应用条件的理解，满足条件的不同题目中尝试使用，在考试中可以提高做题的效率，得到更多的分数。
